Using Beginner's Mind and Maximum Entropy to understand Emptiness

This post is part of the Mystical Entropy project at Leiden University (funded by the Templeton Foundation) and an evolution of some of the key ideas in my recent book, Psychedelic Experience: Revealing the Mind.

The main line of thought I will develop here is that we can analyse the notion of beginner’s mind using the concept of entropy to arrive at a particular way of understanding śūnyatā, otherwise known as emptiness. Although emptiness is ineffable, we can nonetheless use words to point to it, and that’s the main goal of this post: to point to emptiness using entropy.

To get going, I will explain beginner’s mind and the principle of maximum entropy (section 2 and section 3). I will then stick these two ideas together to show how we may understand the former in terms of the latter (section 4). However, there will be a twist: we will see that this line of reasoning leads us to an infamous paradox in information theory (section 5). That paradox will then provide us with a focal point through which we can understand the nature of emptiness (section 6).

2. Beginner’s Mind

The phrase “beginner’s mind” was popularised by Shunryū Suzuki in his 1970 classic Zen Mind, Beginner’s Mind (one of my all-time favourite books).

Suzuki’s teaching was that the way of Zen can be understood as the cultivation — or rather the revelation — of a mind that is alert, open, and pure. This mind, this Zen Mind, is like that of someone beginning to study some subject for the first time, except that the Zen mindset applies to everything, and not just some limited domain of inquiry. According to Suzuki, such a mind is free, available for anything, and — crucially — a vehicle for the expression of one’s true nature. Thus, central to Suzuki’s teaching was the principle that cultivating a generalised beginner’s mind is the essence of Zen practice — and a very good thing to do. Let’s call this principle, Beginner’s Mind.

Although Beginner’s Mind is now commonly attributed to Suzuki, the basic idea can be found elsewhere in Zen Buddhism. For example, it appears as Don’t-Know Mind in the teachings of Seung Sahn in Korea’s Seon Buddhism (1927-2004) and as Great Doubt, Great Awakening in the teachings of Boshan in China’s Chan Buddhism (1575-1630). Going back even further, we also find the advice:

in the 6th century text Xinxin Ming by Jiànzhì Sēngcàn, the Third Chinese Patriarch of Chan.

Indeed, Beginner’s Mind is not exclusively a Zen principle since we can trace basic the idea through other Buddhist traditions and, indeed, through other precursors of Zen, such as Daoism, Confucianism, and early Vedanta. For example, Chapter 71 of the Dao De Jing says:

And a verse of the Kena Upanishad (circa 6th-4th C. BCE) says of Brahman:

We also find a very similar idea in Plato’s dialogues: Socrates was wise in that he didn’t make the mistake of thinking that he knew something when he did not. Armed with his probing method of elenchus, Socrates regularly induced states of aporia — profound states of wonder and uncertainty — in his interlocutors, and Plato often presented this as a good thing for their wellbeing (for example, in Meno 84a-c). And, a little later in the West of Greece, the Pyrrhonian skeptics were famously cultivating ataraxia, a mental state of tranquility and equanimity arising from an embrace of uncertainty.

To be sure, this isn’t to say that Beginner’s Mind is universal among the world’s philosophical/spiritual/mystical/wisdom traditions. However, it is quite common. For example, we also have the Cloud of Unknowing in Christian mysticism (Johnston 1973) and the notion of a “child mind” in Hasidism (Shonkoff 2023). Daniel Batson has also recognised the role of doubt and openness in his notion of quest religosity (Batson 1993). Thus, although it may not be universal, we often find something like Beginner’s Mind playing a salient — and even fundamental role — in these traditions.

We can also find secular examples of Beginner’s Mind — or rather examples of its absence. For example, cognitive psychologists have found that most people tend to suffer from overconfidence, the widespread metacognitive bias of being too confident in one’s beliefs:

Indeed, in an interesting alignment with the Dao De Jing, some recent research indicates that overconfidence may spread in human populations like an infectious disease (Cheng 2020). Not surprisingly, research also indicates that there may be methods for reducing overconfidence in people (e.g., Speirs‐Bridge 2010). Another example from cognitive psychology is the Einstellung effect, whereby a person becomes so accustomed to a certain way of doing things that they are unable to consider or acknowledge new ideas or approaches. Unfortunately, it seems that the default condition for the human mind is one of overconfidence and accustomed habit. (An exception that helps prove the rule is Amazon’s perpetual Day One mentality.)

I think this is why we find Beginner’s Mind playing such an important role in so many of the world’s wisdom traditions. Recognising the “sickness” and prevalence of overconfidence, each tradition developed methods for treating it. For example, the primary method for Socrates was his constant questioning and challenging of the opinions of those around him. In Zen, it has been the practice of zazen — “just sitting” meditation — and the contemplation of koans (designed to help the mind’s certainties self-destruct). There are many methods, but the thread running through them is the insight that a good way to discover wisdom is to let go of one’s supposed knowledge and become comfortable with resting in uncertainty.

A common objection to all of this is that, although we may suffer from overconfidence, we do in fact know things. Moreover, the knowledge that we have managed to cobble together as a species is incredibly valuable. It would be foolish to abandon this knowledge… so the objection goes, often accompanied by a thump of the table and a “Behold our STEM!” exclamation:

However, this objection is based on at least two mistaken assumptions. First, science is more in the business of uncertainty than people tend to think (see here, for example). Second, cultivating a beginner’s mind doesn’t necessarily lead to the abandonment of all knowledge. Rather, we can think of it as the practice of recalibrating one’s beliefs to reality. As Suzuki put it:

Thus, it is entirely compatible with Beginner’s Mind to continue relying on expert medical advice, traffic lights, etc. At the same time, it can be surprising what one is willing to discard and how liberating and beneficial this can be.

This is an important point. Many psychological disorders — such as generalised anxiety, obsessive-compulsive behaviour and thinking, and depressive rumination — appear to be driven by an intolerance of uncertainty (for a recent review, see Sahib 2023). Since the practice of Beginner’s Mind involves becoming comfortable with uncertainty, it stands to reason that it may help with the prevention (or perhaps treatment) of such disorders. Moreover, an intolerance of uncertainty can also stall one’s spiritual development, since it is a comfort with uncertainty that allows for higher forms of wisdom to appear to the mystic:

Thus, we can extract three important ideas from Beginner’s Mind. The first idea is that Beginner’s Mind is good at preventing the various kinds of suffering that arise from an underlying intolerance of uncertainty. The second idea is that Beginner’s Mind is good for practical situations, such as creative-problem solving and reducing overconfidence (escaping the Einstellung effect, for example). The third is that the practice of Beginner’s Mind is essential to making spiritual progress — a person can become stuck on their spiritual path when they start to think they know things.

Now that we have completed Beginner’s Mind 101, let’s switch gears and consider the principle of maximum entropy…

3. Maximum Entropy

To understand the principle of maximum entropy, we first need to acquaint ourselves with The Three Basic Ideas of Bayesian Epistemology.

The First Basic Idea is a claim about human psychology. It says that humans don’t always believe things in a binary, black-and-white fashion. For example, I don’t believe outright that it will be sunny in Amsterdam today, but I suspect it will — indeed, I’m more confident than not. Thus, Bayesian epistemology says that we should recognise that our beliefs come in degrees.

In what follows, to make it clear that I am talking about a degree of belief rather than a full, outright belief, I will use the term that has become standard in the literature: credence. For example, my credence that it will be sunny in Amsterdam is higher (or stronger, if you like) than my credence that it will be cloudy.

The Second Basic Idea is a claim about what it takes for one to be rational. It says that one’s credences should satisfy the axioms of probability theory.

For example, suppose my credence that it will be sunny in Amsterdam today is 80%. The probability axioms then entail that my credence that it will be cloudy — i.e., that it won’t be sunny — in Amsterdam today should be 20%. This is because probability percentages should sum to 100%. As another example, if my credence that it will be sunny in Amsterdam today is 80%, then my credence that it will sunny in the Netherlands today should be at least 80%. This is because “sunny in Amsterdam” is only one way for it to be “sunny in the Netherlands”, and so my credence concerning the latter ought to be at least as high as that for the former.

The Third Basic Idea is another claim about rationality. However, whereas the previous claim was synchronic, in that it makes a claim about how your credences should be at any given time, this second claim is diachronic in that it makes a claim about how your credences should change over time. In particular, this Third Basic Idea says that when one learns new information, one’s credences should adjust according to an updating rule known as conditionalisation.

To illustrate how this works, it will help if we imagine that we’re now inside the Holland Casino…

Imagine you look over at me playing craps from your poker table and see that I’ve just rolled the dice. What should your credence be that the dice landed with two “sixes” facing up? Knowing that the casino’s dice are fair, your credence ought to be 1/6 x 1/6, which is 1/36, or 2.78%. Now suppose I yell over to you that one of the dice landed with its “six” facing up. Given this new information, what now should be your credence that both dice landed “sixes”? According to the rule of conditionalisation, your new credence should be 1/6 (or 16.67%), quite a bit higher than your previous credence of 1/36 (2.78%). This is because my yelling to you that one of the dice landed “six” gave you new information that should strengthen your credence that both dice landed “sixes”.

These Three Basic Ideas provide the foundation for Bayesian epistemology, which is an extremely powerful framework for managing uncertainty and conducting rational inference, including everything from scientific research to everyday reasoning.

However, there is a problem.

Although Bayesian epistemology tells us that our credences should satisfy the probability axioms and change when we learn according to conditionalisation, the framework doesn’t tell us what our credences should be initially.

This is known as the problem of the priors. The problem is that our initial credences — our “priors” — can have a huge impact on the conclusions we draw from our evidence, and yet Bayesian epistemology gives us almost no guidance concerning what those initial credences should be.

That is a big problem if we are committed to the idea that science and rational inference are meant to be endeavours that guide us towards objective truth. Indeed, using the framework, we can prove so-called Bayesian convergence theorems: roughly speaking, no matter how much evidence we ever manage to acquire, there will always be two sets of initial credences that deliver arbitrarily different conclusions (posteriors), even though they both obey the probability axioms and conditionalisation. Effectively, this means there is no way to rationally criticise anyone we disagree with. A flat-earth conspiracy theorist can be just as rational as someone who “follows the science” (and vice versa).

That is a not good outcome for a theory of knowledge and rationality!

So, over the years, many philosophers and statisticians have attempted to address this problem in a variety of ways. I won’t go into all the details here, but roughly speaking, these academics tend to fall into two camps: Subjective Bayesians and Objective Bayesians.

The Subjective Bayesians say that we should learn to embrace this subjectivity and that it isn’t so bad. However, although such a view might seem fine in the abstract, when the time comes for us to take a medication that may have nasty side effects, we tend to find that we want our doctors to base their advice on objective reality rather than their subjective whims. Indeed, people die all the time because of dodgy statistics. That seems like a bad thing that we should try to avoid. Thus, many philosophers and statisticians have a strong intuition that our theory of rational inference and uncertainty ought to have some kind of objective grounding.

Not surprisingly, the Objective Bayesians are motivated by that intuition, and so they look for a way to make Bayesian epistemology more objective. This is where the principle of maximum entropy, which I’ll call Maximum Entropy, comes into play.

The intuitive idea behind Maximum Entropy is that we should be intellectually humble and refrain from having credences that are not supported by evidence or reason. At the same time, our credences should be grounded in any knowledge that we genuinely have. Put another way, the principle says that one’s credences should perfectly reflect one’s genuine knowledge and otherwise remain as uncertain as possible.

That “remain as uncertain as possible” bit is the core feature of Maximum Entropy. This is because, in this context, entropy reflects the overall uncertainty of one’s credal distribution (i.e., all of one’s credences).

For example, if I am only 50% confident it will be sunny today, then I am more uncertain about today’s weather than someone who is 80% confident in that proposition. My 50%-50% credal distribution has greater entropy than their 80%-20% distribution. In fact, because entropy can be defined with a mathematical formula, we can calculate precisely the levels of entropy associated with these credal distributions. In this example, the entropy associated with my 50%-50% distribution is 0.69 and, for the other person’s 80%-20% distribution, the entropy is 0.5. Generally speaking, the flatter or more uniform one’s credal distribution, the higher one’s entropy — one’s overall uncertainty.

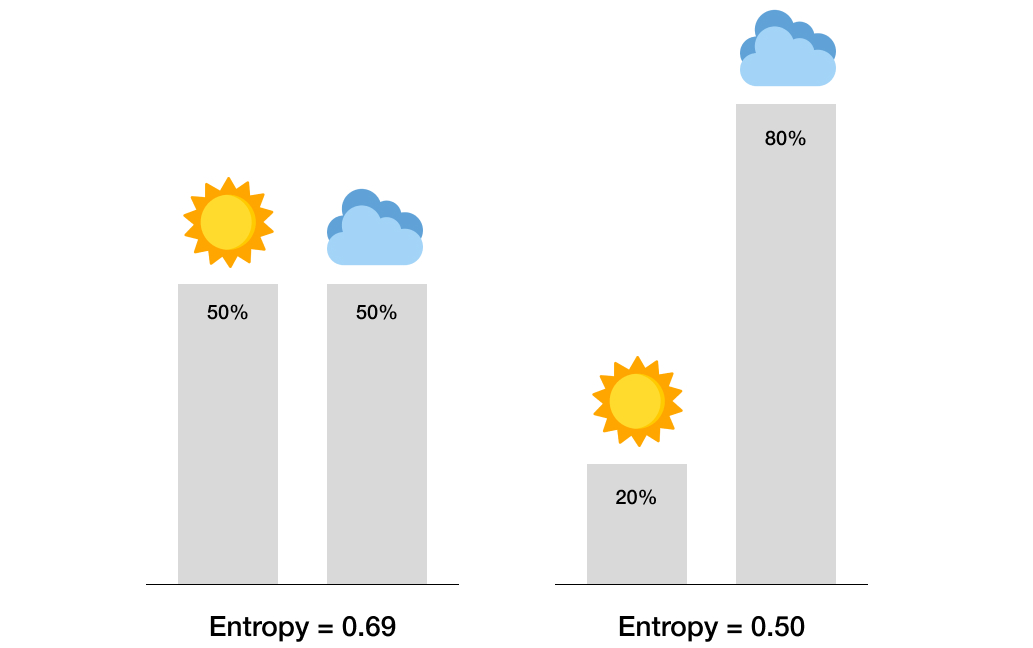
To summarise, Maximum Entropy says that one ought to have credences that are as uniform (“flat” or “even handed”) as possible and that they should only depart from this uniformity if one has genuine knowledge in support of that departure. There are three main advantages to this principle. First, it appears to bring objectivity back to Bayesian epistemology, thus making it more suitable as a theory of scientific and rational evidence. Second, Maximum Entropy has a lot of intuitive appeal since its guiding intuition is that we shouldn’t have credences that are based on unwarranted assumptions. Third, the principle appears to work — it has many practical applications in all sorts of domains, from physics, to biology, to climate modelling, to our global communication systems. Indeed some of the applications of Maximum Entropy are so successful that they can have a magical feel to them (Jaynes 1973).

Okay, so that completes Maximum Entropy 101. Let’s now see if we can use Maximum Entropy to understand Beginner’s Mind. If we can, then we will be able to establish an important point of conceptual contact between science and the mystical traditions.

4. Zen Mind, Entropic Mind

We have two principles in hand, Beginner’s Mind and Maximum Entropy. Although the traditions they come from are very different, the two principles share a lot in common. In particular, both principles capture the importance of being explicitly aware of one’s uncertainty, of learning from experience. Thus, there could be a lot to learn from understanding Maximum Entropy as a mathematically precise statement of Beginner’s Mind.

If we equate Beginner’s Mind and Maximum Entropy in this way, then we establish a fruitful point of contact between two of humanity’s major systems of thought — what we may loosely call mysticism in the East and science in the West. I think we can use this conceptual bridge to transfer valuable ideas between the two systems of thought.

For example, if a mystic claims that meditation tends to be good for cultivating a beginner’s mind, then the scientist can check this by assessing how a subject’s credal distribution tends to change over the course of their meditative practice. That is, we should be able to observe that meditator’s credences tend to become better calibrated over time. Assuming that people tend to start off overconfident, this improvement in calibration will manifest as an increase in the entropy of their credal distributions.

Indeed, there is some evidence for this already. For example, Lakey 2007 found that mindfulness was negatively associated with overconfidence among frequent gamblers. More recently, Charness 2024 observed a three-month meditation training program reduced overconfidence (and improved other measures of cognitive performance). Another recent study found that a two-week meditation course reduced information avoidance (Ash 2023). Less directly, but still highly relevant, is the observation that many of the qualities of so-called superforecasters — people who are unusually good at making accurate probabilistic predictions — are qualities of a beginner’s mind. For example, two such qualities are (i) being open to evidence and (ii) being able to change perspectives (Tetlock and Gardner 2015).

To give another example, if a mystic were to claim that cultivating a beginner’s mind tends to be good for well-being, then the scientist can check this by assessing whether calibration (lack of overconfidence) is an indicator of well-being.

As before, there is some evidence in support of this. For example, there is a large literature centred around the idea that uncertainty intolerance is a driving force behind many psychological disorders (Boswell 2013). Indeed, growing evidence indicates that mindfulness-based interventions can reduce the symptoms of such disorders and that these reductions are mediated by reductions of intolerance of uncertainty (Papenfuss 2022). Interestingly, one study found that subjects became more reliable forecasters of their life events (i.e., improved calibration) after psilocybin-assisted psychotherapy for treatment-resistant depression (Lyons and Carhart-Harris 2018). It should be noted, though, that there is some evidence against the idea. For example, the “sadder but wiser” hypothesis that emerged in the 80s says that depression enhances calibration because depressed people see the world more accurately (Alloy and Abramson 1979). However, although this hypothesis is widely accepted, the evidence for it is not convincing. Indeed it has failed to replicate in several studies (Dev 2022). Clearly more work needs to be done, but the main point here is that it should be possible to empirically verify the mystics’ claim that cultivating a beginner’s mind tends to be good for well-being.

These are two examples of how we can use the bridge to go from East to West. Can we also go in the other direction? I think so…

For example, one problem that many mystical traditions grapple with is how to scale their teachings without them becoming corrupted over the centuries. This problem arises from the fact that many of the ideas and practices of these traditions are counterintuitive, ineffable, and surprisingly powerful. So it is easy for things to go bad — cults can form, for instance. Thus, many traditions try to establish a system of quality assurance — for example, by protecting the teachings with secrecy and only giving them to sufficiently prepared students. This works, but it isn’t perfect since the secrecy is not always honoured and monastic integrity can devolve over time (like any other human institution with power). Therefore, one way to help address this issue might be to introduce objective evidence into these systems — alongside their traditional expert asseessments. The idea is that objective measures of spiritual progress (that can be replicated and validated by anyone) may facilitate the teaching of mystical wisdom at greater scale and with greater quality.

As another example, it is also possible that science could eventually help with the development of new spiritual technologies. Many mystical traditions are living systems of thought — they are constantly being updated and adapted to new environments — and so it is possible to find innovation within them. The evidential precision of science could assist that innovation in ways that we have never seen before. Obviously that is getting ahead of things a bit, but it is an example of a benefit that science might be able to bring to mysticism.

Overall, we seem to be in a very pleasing situation in which philosophical theory and empirical evidence are in alignment — and have the potential to result in substantial benefits. Thus, this Maximum Entropy analysis of Beginner’s Mind is a nice example of how we can use the concept of entropy to translate an important idea from the mystical traditions into the language of science to form empirically testable hypotheses with strong theoretical motivation. The guiding idea behind the Mystical Entropy project is that this is just one example of such a translation. We should be able to find many more if we study these traditions carefully (see here for some other examples).

5. Paradox!

This may sound all well and good, but it turns out that so far we are only scratching the surface. When we dig a bit deeper, we find some problems. However, those problems turn out to be weirdly desirable. Let me explain… In this section I’ll present the problems and in the next section I’ll explain why we should see them as features, rather than as bugs.

As we saw in section 3, the principle of Maximum Entropy has a lot of intuitive appeal. However, it doesn’t quite do what it is purported to do. Although it is useful in a wide variety of applications, it isn’t actually an objective method for determining prior probabilities. This may not be apparent in typical applications of the principle. However, we can observe the subjectivity of Maximum Entropy manifest when we try to apply it in cases that involve greater uncertainty. To see this, let’s consider the following two thought experiments…

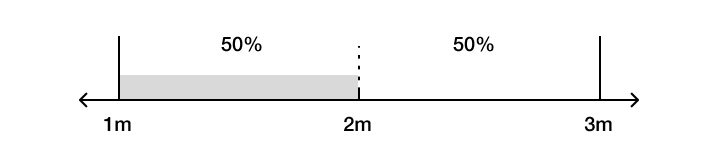
First, imagine a factory that produces cubes with side lengths between 1 and 3 metres… What is the probability that the next cube that the factory produces has a side length between 1 and 2 metres? The intuitive answer that most people give is 50%. This is because having a side length between 1 and 2 metres takes up half of the full possibility space (1 to 3 metres). This assignment is also what we get from Maximum Entropy, which tells us to assign a uniform probability distribution over the space of all possible cubes that the factory may produce.

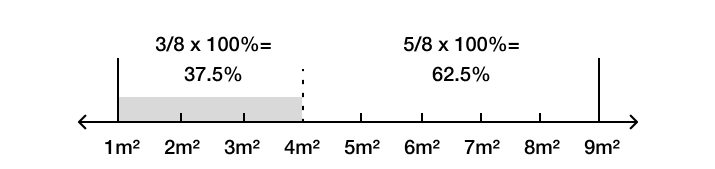
Second, now imagine a factory producing cubes with face areas ranging between 1 and 9 square metres… What is the probability that the next cube that the factory produces has a face area between 1 and 4 square metres? This question is a little trickier than the first, but after some reflection most people give the answer of (4-1)/(9-1) = 3/8, which is 37.5%. And, as before, this is also the probability that Maximum Entropy tells us to assign.

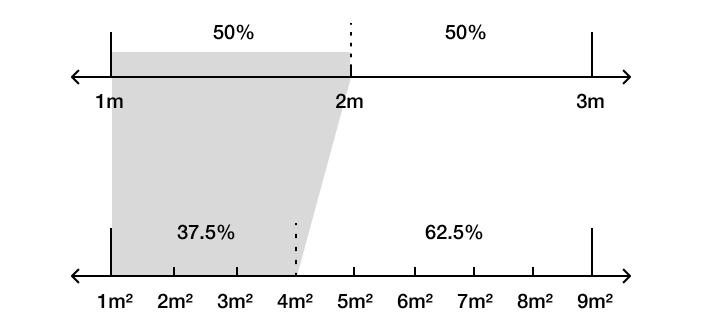
These are two seemingly straightforward applications of the Maximum Entropy principle. However, there’s a problem. The problem stems from the fact that the two thought experiments are actually one. This is because a cube having a side length between 1 and 3 metres is also a cube with a face area between 1 and 9 square metres. And the problem is that Maximum Entropy assigns two different probabilities to the same event. This happens because having a side length between 1 and 2 metres is the same as having a face area between 1 and 4 square metres.

It is tempting to dismiss this problem as philosophical pedantry or some sort of mathematical trickery. However, this problem has been of great concern to physicists working on the foundations of statistical mechanics, and despite several attempts to address or dismiss the problem, it stubbornly persists to this day. It also has real-world, practical implications because the problem can influence everyday decision-making. This effect is known as partition priming: the judgements and decisions that people make are influenced by how their options are partitioned (Fox and Clemen 2005).

The essence of the problem is that what counts as maximally uncertain (entropic) depends on how you conceptualise the world. On one way of looking at things, a uniform probability distribution over side lengths maximises entropy, and on another, a uniform probability distribution over face areas does. And, of course, there is an infinite number of other ways of conceptualising the world. Indeed, for any arbitrary probability assignment we might choose, there is a way of conceptualising the cube factory such that Maximum Entropy would “justify” that assignment. That way of conceptualising the cube factory may be rather strange, but it nonetheless exists, and there’s nothing about Maximum Entropy or the rest of Bayesian epistemology that rules it out as impermissible.

Another way of summarising the problem is that your true uncertainty is not representable by a probability function. This is because any probability function takes a stand on some issue that goes beyond the knowledge you have, even though this may not be immediately apparent. For example, the uniform probability function over side lengths looks like it is perfectly agnostic if we only think in terms of side lengths, but when we reframe the problem in terms of face areas, we see that it has a particular bias to it (roughly speaking, it says that cubes with larger face areas are more likely than those with smaller face areas). To put the point in yet another way, there’s an ineffable aspect to your uncertainty — your state of uncertainty is not expressible in the language of probability theory. That is, any attempt at probabilistically representing your uncertainty necessarily involves a distortion of it. This fact, that uncertainty cannot always be quantified in terms of probabilities, has been recognised by many authors and received many names. The distinction between probability (risk) and uncertainty was first made by Keynes 1921 and Knight 1921, with the subsequent literature often refering to the distinction as between uncertainty and deep or Knightian uncertainty. The latter has also been called structural uncertainty (Pacchetti 2021), and even wild and feral uncertainty (Ramírez and Ravetz 2011).

Although we’ve been using probability theory to appreciate this ineffability of uncertainty, it is not a problem peculiar to the use of probabilities (or Bayesian epistemology). The cube factory thought experiment is closely analogous to Nelson Goodman’s new riddle of induction (Goodman 1955), and the essence of the general problem has its roots in David Hume’s problem of induction (Hume 1739). As Hume famously argued, we may be justified in our inductive inferences, but we can’t articulate what that justification is. As Titelbaum 2011 has shown, this problem arises for any theory of uncertainty that satisfies very minimal and intuitive constraints. The title of the paper in which he proves this result is rather apt: “Not enough there there”, alluding to the problem being that evidential propositions do not possess enough information to objectively determine which hypothesises they support. The upshot of this result is that we always introduce some subjective element when we, for example, claim that some evidence favours one hypothesis over another (or favours them equally). In other words, when we carefully examine the foundations of scientific inquiry, we find that there is not enough there there.

This problem has been rather disturbing for many philosophers and scientists. It is a basic assumption of science that the future will be like the past, and yet we have absolutely zero guarantee of that. (Appealing to the past successes of science is obviously circular.) This is why C.D. Broad referred to inductive inference as the glory of science and the scandal of philosophy (Broad 1926). The success of science depends on inductive inference and yet philosophers can’t find a way to give induction the epistemic foundation that it seemingly deserves. Indeed, the problem is worse than that: Hume 1739 gave a very elegant and convincing argument that it is impossible to fully justify our inductive inferences. We want the situation to be otherwise, and some of us have very strong intuitions that it is otherwise. But it simply ain’t. In my opinion, this philosophical problem is right up there with the hard problem of consciousness (Chalmers 1995). We could even call it the hard problem of uncertainty.

6. Emptiness: There is no there there

We’re now in a weird situation. First of all, we just a saw a legitimate paradox. And those tend to be weird. Indeed, this one is especially weird since it occurs in the very foundations of science. What’s weirder still, though, is that we can use this paradox to understand a fundamental idea we find in many of the world’s mystical traditions.

This idea — if you can call it an idea; it is also like an experience — is ineffable. Moreover, it is ineffable in the deepest possible sense of that word. All experiences are ineffable in that language cannot fully capture them. However, this “experience” — remember it is also like an idea — is especially ineffable. You might even say that it is maximally ineffable. Going into this issue requires a longer discussion, which you can find in Chapter 11 of my book. For now, it suffices for us to note that we can, in fact, kind of talk about this idea — so long as we constantly remember that we are talking about the untalkable.

Many of the world’s mystical traditions have developed sophisticated ways of understanding this idea/experience. For example, in Buddhism it is known as śūnyatā, which is often translated as “emptiness”, but it could also be translated as “spaciousness”. In Yoga, it is known as Shiva or Brahman, which are sometimes characterised as “pure consciousness” and “absolute reality”. In Daoism, it is known as wu or wu-wei, which are commonly translated as “nothingness” or “non-being” and “non-doing” or “effortless action”. In Sufism, it is known as Fana, the annihilation of ego that allows for a realisation of unity with ultimate reality and a flowing of the Divine. In Platonism, it is the Form of the Good, which is the highest form of reality — ineffable, eternal, ethereal, etc. And so on. The same idea appears to show up all of over the place.

Do we know if it really is the same idea in all of these traditions? Perennialists say “yes” and Contextualists say “no”. Fortunately, it doesn’t matter because we can use our paradox to point us at any one of these ineffable notions. Pick your favourite one and what follows should work. To illustrate, I’ll work with śūnyatā; however, the same kind of philosophical manoeuvring can be applied to the other examples.

What is śūnyatā? The term ‘śūnyatā’ is traditionally understood to be composed as ‘śūnya-tā’, where ‘śūnya’ means “empty” or “void”, and so ‘śūnya-tā’ would mean “emptiness” or “voidness”. Those meanings can sound negative or nihilistic to some people, so I think it can also help to think of śūnyatā as “spaciousness”, which helps convey the delicious freedom that can be found in the idea/experience. At any rate, I’ll stick to the common translation of ‘śūnyatā’ as “emptiness”.

So, what is emptiness? Emptiness is ineffable. However, in our current context, we may understand it as the insight that:

• Reality is beyond all conceptualisation.
• Thus, all conceptualisations distort reality (introducing different forms of maya or “cosmic illusion”).

This insight may sound metaphysically abstract, and it is, but it also has all sorts of important practical consequences.

We can begin to see this by noticing how emptiness is the feature of reality that drives the cube-factory paradox. Clearly, we can conceptualise the cube factory in different ways. For example, in my presentation of the paradox, we can conceptualised the factory in terms of (i) side lengths and (ii) face areas. And notice that neither conceptualisation is superior to the other. In fact, they are equivalent in an importance sense, since area = length² and length = area^1/2. Nonetheless, we saw how these two conceptualisations drove the principle of Maximum Entropy to generate different opinions about the factory’s next cube. To make matters worse, these lengths and areas are not the only games in town. For example, we could have chosen volumes instead. Indeed, we could choose any one-to-one correpspondence function — length + sin(length), for instance, would also work. (You can define even weirder choices using piecewise functions.)

Importantly, as I mentioned before, this problem also appears in everyday decision-making. It happens in different ways, but a salient one is the partition priming of decisions (e.g., Fox and Clemen 2005). How we conceive or view reality affects our opinions in ways that are often invisible to us — but nonetheless measurable empirically. We can reveal the effects of unconscious dispositions to ourselves using carefully defined thought experiments, like that of the cube factory. This can help us have an insight into the arbitrary nature of our opinions and experiences. However, the insight remains mostly at the level of propositional understanding, and so it has a kind of shallowness to it. This can be corrected somewhat, since the more you imagine yourself actually having to grapple with the cube-factory (more on imagination in a moment), the more experiential, and thus deeper, the insight becomes. Nonetheless, the insight is still narrow in an important sense, since it remains focused on the cube-factory and influenced by our meta-conceptualistions (for example, in addition to lengths and areas, we’re also using probability theory). That narrowness limits how deep the insight can go.

Fortunately, Buddhists (and other mystics) teach us that we can understand this insight with far greater depth and generality via the practice of meditation. (In my book, I argue that we can also use psychedelics to assist this meditative project.) That deeper and more general form of the insight is the insight of emptiness. The main point I want to offer in this blog post is that one can guide one’s meditation towards the insight of emptiness by contemplating the cube-factory paradox (or any of its information-theoretic cousins). That is, the paradox provides a convenient focal point through which one can meditate into a deeper and broader understanding of emptiness.

So, instead of viewing the paradoxical nature of entropy as a bug (as many philosophers have), I think we should be seeing it as a feature. It’s only a bug if we forget it exists — or try to pretend it doesn’t exist. Moreover, if we’re willing (and able) to remain aware of it, then we can even benefit from it.

This is because if every conceptualisation distorts reality, then there isn’t a single “true” conceptualisation, and so we have some freedom to choose a conceptualisation that suits us best. This freedom to choose alternative conceptual schemas is often at the heart of major scientific advancements. Einstein’s theory of relativity is a famous example, but there are many others — for example, those documented in Kuhn 1962. So, at least when it comes to reflecting how good scientific inferences are made, the flexible quality of Maximum Entropy is potentially a good thing, not a bad one.

It also allows us to develop a more sophisticated analysis of Beginner’s Mind. While those who regularly practice engaging a beginner’s mind may have better probabilistic calibration, we should also be able to observe a greater willingness of such people to switch conceptual schemas. That is, it is part of Beginner’s Mind that one should also practice having a beginner’s mind with respect to how one conceptualises reality. Indeed, there is some evidence that suggests this may be true. For example, Vervaeke and Ferraro 2016 give a nice review of how meditation and related mindfulness practices can enhance frame-breaking and cognitive flexibility. It also appears to be what is happening with psychedelic-assisted therapy — people tend to discover new ways of reframing their life experiences (their evidence) leading to greater well-being (Letheby 2021).

Furthermore, we should also observe that such people tend to think using relatively simple ideas and concepts. If one conceptual schema is simpler than another and differs in no other way, then why not choose the simpler one? The simpler conceptual schema is easier to use, and so more efficient — more economical. Not only can we use this to as another factor when empirically measuring how beginner a particular mind is, we can also use it to see how this mental quality relates to well-being. The less effortful it is for one to navigate the world, the better off one will tend to be (all else being equal). Yet another consideration in this regard is that simplicity also helps protect against overfitting, and thus would be a factor that drives accuracy. A similar point can be made abut the generality of one’s epistemic system (but I won’t go through that here).

Overall, for people who regularly practice engaging with a beginner’s mind, we should be able to observe higher levels of calibration, accuracy, simplicity, generality, and flexibility.

One worry about embracing emptiness in one’s epistemology in this way is that it can seem to give us too much freedom. That is, the freedom of emptiness might appear to allow for the subjectivity that Objective Bayesians are trying to avoid. More specifically, the paradoxical quality of Maximum Entropy makes the theory so flexible that you can always find a prior to deliver the posterior you happen to wish for. Indeed, Bayesian theories in general have been criticised for being too flexible in this respect (e.g., Bowers and Davis 2012).

However, this freedom is constrained by our limited creativity and cognitive capacities. In some cases, it is relatively easy to find equivalent conceptualisations deliver different Maximum Entropy probabilities. For example, we saw this in the cube-factory thought experiment — I used lengths and areas to make the point, but I could have also used volumes. However, it is not always so easy to find such alternative conceptualisations. Indeed, we can see this even in the cube-factory thought experiment. I could have used lengths, areas, and volumes… but what else? We have to get a little creative to find the other conceptualisations. For example, we could also use hypervolumes (lengthⁿ), but that’s kind of an unnatural thought to have. There are still more conceptualisations — infinitely many, in fact. However, they get weirder and weirder. For example, here’s another one: length + sin(length). Most people would never consider thinking about the cube factory in these weird ways (including hypervolumes), naturally putting a limit to their epistemic freedom.

Normally that would be considered a bad thing. However, I think in this case it is a virtue. Recall the Bayesian convergence theorems from Section 3. Roughly speaking, they say that as we collect ever-more data, any differences between priors tend to wash out over time. That means, as the evidence accumulates, you have to get even more creative to find different priors that drive meaningful differences. And if you’re only creative enough to think of lengths, areas, and volumes, then it will be relatively easy to collect enough data to wash out any differences between those conceptualisations.

Moreover, even if you are creative enough to think of something like length + sin(length), that only means you are capable of thinking of that conceptualisation. It doesn’t entail that you will — or should — think of it on any given occasion. Even the most creative of people are still finite beings with urgent priorities. Suppose you happen to not care about cube factories (such people exist, apparently). Then, since you don’t care, you won’t put much thought into my questions about their lengths, areas, etc. And even if you did somehow slightly care, you’ll probably wait a while before acting on any probabilistic assessment, so you can see what kinds of cubes the factory tends to produce.

Okay but what if you do care and you do put the effort in, then what? Well, you can wait for some data to come in. Yes, that data may not suffice to wash out the differences. However, it may suffice to start bringing some conceptualisations more into agreement with each other than others. And if the disagreeing ones tend to be the creative ones, then intuitively they become less of a concern. Moreover, if the data do not even suffice for this, then there are still things you can do. For example, you can use Maximum Entropy to assign prior probabilities to the resulting accuracy scores of the conceptualisations. This could be a uniform distribution, or it could bias some conceptualisations over others based on their track records. Although the subjectivity never quite goes away completely, it does become increasingly irrelevant and difficult to find.

So far we have been focused on conceptualisations that are equivalent to each other. However, this constraint is by no means entailed by emptiness. There’s no reason why completely radical, seeming impossible, conceptual schemas can be used. However, it is easy for those alternative schemas to be defective in some way — usually they become too complex and unweildy and/or they suffer in terms of empirical adequcy (e.g., similar to Ptolemic epicycles). There are exceptions of course. Einstein’s theories of relativity and his discovery of E=mc^2 are beautiful examples of novel reconceptualisations that resulted in greater generality and empirical adequacy.

We can also use alternative conceptualisations to create useful imaginaries. A useful imaginary is an alternative reality that you experience as real and gives you a much-needed cognitive flexibility that you wouldn’t otherwise have (at least, not easily). We have things like this in information theory, actually. For example, Fourier transforms can be used to simplify signal processing, and the mathematics of these transforms is made much easier with the use of complex numbers, which are combinations of real and imaginary numbers. It is important to understand that the word ‘imaginary’ in this context shouldn’t be understood to imply the numbers aren’t real. In mathematics, if real numbers are real, then imaginary numbers are real too. So, why do we call them imaginary? Basically because when imaginary numbers were introduced in the 17th century, mathematicians at the time thought they were so weird that they couldn’t possibly be real. Fast forward 400 years, and now imaginary numbers are widely considered indispensable to physics. (There’s much more to say about this example, but that would be a digression.)

Importantly, many tantric (and shamanic) practices make use of this “useful imaginaries” technique. For example, in Tantric (Vajrayana) Buddhism, mandalas are used as portals into other spiritual realities and the six realms of samsara can be a particularly motivating container for one’s spiritual practice. One way to think about these practices is that they combine the freedom of emptiness with the power of the placebo effect.

Indeed, if psychedelics work by enhancing the placebo effect (Hartogsohn 2016), then their effectiveness at treating certain conditions could understood in terms of them making it possible for people to enter an imaginary space that feels real and thus, via the placebo effect, helps them heal and transform in deep and fundamental ways (Lyon and Farennikova 2022). Similarly, although staring into an alternative spiritual reality through some coloured paint may seem imaginary (in the “not real” sense) to us, those on the other side of this reconceptualisation are adamant that it does have a kind of reality and effectiveness to it. It is just a more subtle reality than the usual base reality that most people are familiar with (in their own ways, of course).

Nonetheless, there is clearly an epistemic risk in engaging with these practices, since not all imaginaries are useful. In fact, most are outright harmful (there are more ways to be dead than alive). Moreover, there is also the risk of becoming stuck in them — just as we are currently stuck in our own conceptual schemas (at least, according to the mystics who understand emptiness). Mitigating these two risks is one of the reasons for the strong emphasis on secrecy and pedigreed teaching lineages in many of the world’s mystical traditions.

I think it is also useful to consider what happens if we let go of any constraint whatsoever on our conceptualisations. When this happens, it becomes much easier to be creative and we start to enter the purely imaginal. The purely imaginal is the dual of emptiness. In their most extreme forms, imaginal practices work with the idea that (apparent) reality is fully optional, and so we can create, or be in, any alternative reality we like (or that happens to rise). Working within those alternative realities can be extremely powerful.

However, with this extreme power comes an extreme risk: it is all too easy to forget that one has drunk the Kool-Aid of their conceptualisation of reality (that is, it is easy to forget emptiness). Indeed, this is one of the main plot elements of Inception: the characters try to use totems to maintain some kind of anchor in base reality. I won’t give away what happens in the movie, but we can easily reason that while totems may mitigate the risk of losing touch with base reality, they can’t eliminate it. This is because totems are themselves imaginaries and so they, too, can lead one astray.

In contrast, tantric practices tend to remain grounded in something. For example, many practices are connected to the breath, which we can think of as the ultimate totem. Even when Morpheus casts doubt on whether it is air that Neo is breathing, it is clear that Neo is nonetheless breathing — something (prāna, perhaps). Moreover, as the practices get evermore sophisticated, there’s a greater reliance on being part of a pedigreed teaching lineage, which is another kind of ground. For example, we see this prominently in the monastic systems of Tantric Buddhism. Being part of a community of practice (a sangha) can be another ground, but it is less reliable and can easily devolve into group think in cult-like behaviour. At any rate, without some kind of reliable quality control, it is all too easy for psychonauts using imaginal practices to become lost in an imaginal maze that simply isn’t useful — and even harmful.

This issue of epistemic risk suggests that science may be of great benefit to the world’s mystical traditions — almost all of which make use of at least some useful imaginaries (tantra has had some influence on many, if not all, major spiritual traditions in the East). The incorporation of (objective) evidence into these traditions creates the potential for a new source of grounding and quality control. Perhaps even more importantly, such a quality control system would be one that scales. The problem with relying on a pedigreed teaching lineage, for example, is that teachers are limited in the number of students that can teach. Also, monasteries can become corrupt when they grow large and powerful (like any other human institution). So, injecting some science into mysticism could be a very good thing — even from the standpoint of the mystics. The Dalai Lama, for instance, has often stated that if science proves certain Buddhist teachings wrong, then Buddhism will need to change accordingly.

However, a fundamental challenge to such an initiative is that the languages of science and mysticism are rather different from each other. And so we have a bit of lost-in-translation situation. This is where our bridge between Beginner’s Mind and Maximum Entropy could be quite fruitful. Making Beginner’s Mind empirically tractable might be enough of a foothold for science to start working its way more deeply into mysticism (some work is already being done, of course, in contemplative science).

In short, by appreciating the full import of the paradoxical nature of Maximum Entropy we can deepen our understanding of the benefits it can transport between science and mysticism. Most importantly, we’ve seen how we can use the concept of entropy to translate a notion we find in the mystical traditions into something that is scientifically tractable…

That’s the general idea for the special issue of Philosophical Psychology that I’m editing with Michiel van Elk on the theme “Mystical Experiences and Entropy”. We welcome submissions from all fields, and if you have any questions (about this post or the special issue), please contact me at contact@aidanlyon.com.